Trigonometry MCQ Mock Test Online Free
Trigonometry MCQs are different types of questions that come in all types of exams. Trigonometry plays an important role in Maths section. If you want to clear your concepts, then you can practice Mathematics introduction online from our website www.sarkarijobalert.com Trigonometry MCQ Test Free Mochak Test. This Introduction to Trigonometry Class 10 MCQs questions examines the understanding and concept of the chapter. You can test your knowledge and evaluate yourself. We suggest that you give as many online free MCQ mock tests as possible so that your concepts can be cleared.
Trigonometry MCQ Online Free Mock Test 1
[ays_quiz id=’19’]
Example Trigonometry MCQ
1) Which of the following is the correct value of cot 100.cot 200.cot 600.cot 700.cot 800?
- 1/√3
- √3
- -1
- 1
Answer: (a) 1/√3
Explanation: Here, we can apply the formula –
cot A. cot B = 1 (when A + B = 900)
= (cot 200 . cot 700) x (cot 100 . cot 800) x cot 600
= 1 x 1 x 1/√3
= 1/√3
So, the correct value of cot 100.cot 200.cot 600.cot 700.cot 800 = 1/√3
2) If tan θ + cot θ = 2, then what is the value of tan100 θ + cot100 θ?
- 1
- 3
- 2
- None of the above
Answer: (c) 2
Explanation: Given tan θ + cot θ = 2
Put θ = 450, above equation will satisfy as,
1 + 1 = 2
So, θ = 450,
= tan100 450 + cot100 450
= 1100 + 1100
= 2
3) If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y
Answer: d
4) If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to
A. 0
B. 1/√3
C. 1
D. √3
Answer: C
5) If θ is said to be an acute angle, and 7 sin2 θ + 3 cos2 θ = 4, then what is the value of tan θ?
- 1
- √3
- 1/√3
- None of the above
Answer: (c) 1/√3
Explanation: Given 7 sin2 θ + 3 cos2 θ = 4
=> 7 sin2 θ + 3 (1 – sin2 θ) = 4
=> 7 sin2 θ + 3 – 3sin2 θ = 4
Then, 4sin2 θ = 1
Or, sin θ = 1/2
So, θ = 300
Now, put θ = 300 in tan θ, we will get,
tan θ = 1/√3
6) Suppose cos θ + sin θ = √2 cos θ, then which of the following is the correct value of cos θ – sin θ?
- √2 cos θ
- √2 sin θ
- -√2 cos θ
- -√2 sin θ
Answer: (b) √2 sin θ
Explanation: It is given that, cos θ + sin θ = √2 cos θ …..(i)
On squaring both sides, we will get,
(cos θ + sin θ)2 = (√2 cos θ)2
=> cos2 θ + sin2 θ + 2 sin θ cos θ = 2 cos2 θ
Or, 2cos2 θ – cos2 θ – sin2 θ = 2 sinθ cosθ
=> cos2 θ – sin2 θ = 2 sin θ cos θ
=> (cos θ + sin θ) (cos θ – sin θ) = 2 sin θ cos θ
=> (√2 cos θ) (cos θ – sin θ) = 2 sin θ cos θ [from equation (i)]
=> (cos θ – sin θ) = 2 sinθ cosθ / √2 cos θ
= √2 sin θ
7) The value of cos 180° is
(a) 0
(b) 1
(c) -1
(d) infinite
Answer
Answer: (c) -1
Hint:
180 is a standard degree generally we all know their values but if we want to go theoretically then
cos(90 + x) = – sin(x)
So, cos 180 = cos(90 + 90)
= -sin 90
= -1 {sin 90 = 1}
So, cos 180 = -1
8) In given figure, the length of AP is
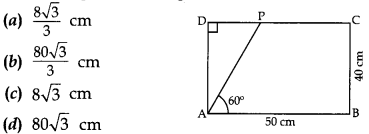
Answer/ Explanation
Answer: b
Explaination:

9) If the value of tanP + secP = a, then what is the value of cosP?
- 2a/a2 + 1
- a2 + 1/ 2a
- a2 – 1/ 2a
- None of the above
Answer: (a) 2a/a2 + 1
Explanation: It is given that, tanP + secP = a ……(i)
As we know, the trigonometric identity, sec2 P – tan2 P = 1 {we assume θ = P}
So, we can apply the formula a2 – b2 = (a – b) (a + b)
=> (sec P – tan P) (sec P + tan P) = 1
=> (sec P – tan P) x a = 1
=> sec P – tan P = 1/a …..(ii)
So, from equation (i) and (ii), we will get –
2sec P = a + 1/a
sec P = a2+1 / 2a
So, cos P = 2a / a2+1 [as sec P = 1/cosP]
10) Which of the following is the correct value of (3 / 1+tan2 θ) + 2 sin2 θ + (1 / 1+cot2 θ)?
- 3
- 9
- 6
- None of the above
Answer: (a) 3
Explanation: (3 / 1+tan2 θ) + 2 sin2 θ + (1 / 1+cot2 θ) = ?
According to the trigonometric identities, the given equation can be written as –
= 3/sec2 θ + 2 sin2 θ + 1/cosec2 θ
= 3cos2 θ + 2 sin2 θ + sin2 θ
= 3cos2 θ + 3sin2 θ
= 3(cos2 θ + sin2 θ)
= 3
